티스토리 뷰
🚀 들어가며...
- 최근들어 BFS, DFS 문제를 풀며 느낀점이 그래프 탐색 문제의 경우 BFS를 쓸지, DFS를 쓸지 감이 잘 안오는 상황이 자주 있었습니다. (경험부족도 있습니다..ㅠ)
이참에 어떠한 키워드나 로직을 발견했을때 어떻게 접근해야하는지 정리를 해보겠습니다!
📑 내용
😎 한눈에 보는 DFS 와 BFS알고리즘의 동작 방법
일단 그림으로 어떻게 돌아가는지에 대해 간략하게 알아봅시다.
# DFS

첫번째로 DFS의 동작 순서입니다. 재귀적인 특징으로 구현을 합니다. DFS는 깊이 우선탐색 알고리즘으로서 선택한 한 루트를 파고듭니다.
#BFS
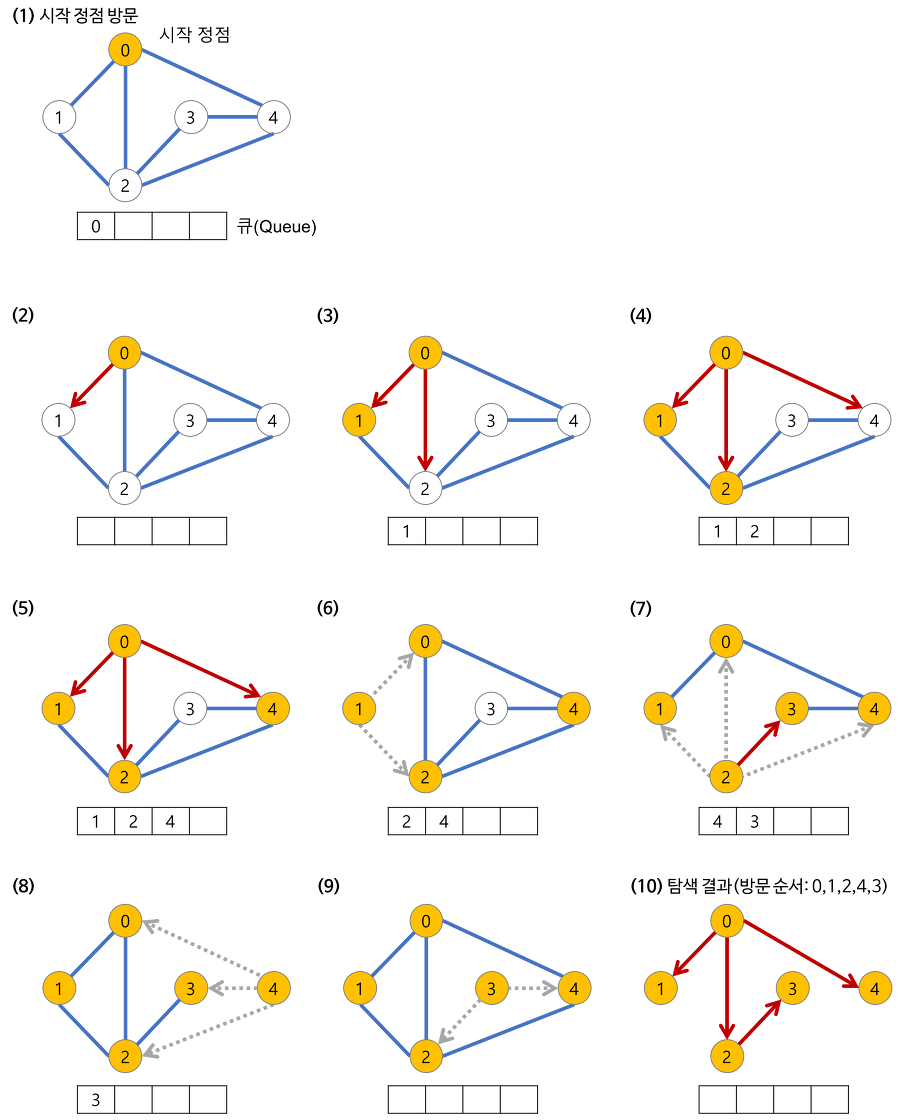
다음은 BFS알고리즘입니다. 큐를 사용해서 탐색합니다.
DFS와 다르게 0번노트에서 시작시 0번에서 갈 수 있는 모든 노드를 1번의 "턴"에 탐색합니다.
여기서 말하는 턴이란 흔히 말하는 depth(깊이) 라고 보시면 됩니다.
위 그림에서 볼 시 2, 3, 4 번의 과정을 묶은것이 한 턴으로 보시면 될것 같습니다.

위 이미지를 보면 확실히 DFS와 BFS는 서로 다른 탐색의 절차를 갖는다는것을 확인 하실수 있습니다.
🤔 그렇다면 DFS와 BFS를 선택함에 있어 어떤 기준이 필요할까
제 개인적인 경험으로(저는 DFS를 더 자주 사용합니다.) 대부분의 경우 DFS와 BFS 어느것을 선택해도 무방한 문제들이 많습니다. (제가 경험한 코딩테스트 수준의 알고리즘)
저는 보통 DFS는 재귀적인 특징과 백트래킹을 이용한, 모든 경우를 하나하나 전부 탐색하는 완전탐색 문제를 풀때 선호하고(대표적으로 조합 순열 구현)
BFS는 depth(깊이)특징을 이용한 문제(대표적으로 최단경로)를 풀어야할때 선호합니다.
🙋🏻♂️ 정리
결론은 간단합니다. 사실 문제를 많이 풀어보면 문제만 봐도 DFS인지 BFS인지 감이 옵니다.
하지만 아직 경험이 부족한 저를 위해 설명한 글이기 때문에 정말 간단히 정리해보자면
DFS
1) 연결된 그래프를 완전 탐색하는데 활용가능
2) 모든 경우를 하나하나 다 탐색을 해야될경우 이용(위의 예의 경우 조합, 순열 모든 경우의수를 하나한 다 찾고자할때)
3) 위의 개념과 결부된 깊이 우선탐색이라는 개념을 가진 순열, 조합 구현에 활용
BFS
1) DFS와 마찬가지로 연결된 그래프를 완전탐색하는데 활용
2) depth(깊이)를 계산해야되는 문제에 활용(위의 문제예의 경우 최단경로의 길이 == depth(깊이))
3) 위의 개념과 결부된 가중치가 같은 그래프에서 최단거리를 찾는데 활용
최단거리라는말 어디서 들어보신적 있으실 겁니다.
그래프 최단거리를 간다는 말은 사실 최단경로를 가는 경우와 거의 동치의 단어입니다.
저희가 보통 배우는 최단경로 알고리즘 하면 딱 떠오르는 다익스트라, 플로이드 와샬 알고리즘인데,
위와 같은 이유로 사실 다익스트라 문제들 풀이를 보면 특정상황에 한정한 경우지만
BFS로 푼 풀이가 심심찮게 올라옵니다.
🔗 참고한 글
https://velog.io/@lucky-korma/DFS-BFS%EC%9D%98-%EC%84%A4%EB%AA%85-%EC%B0%A8%EC%9D%B4%EC%A0%90
DFS, BFS의 설명, 차이점
그래프란, 정점(node)과 그 정점을 연결하는 간선(edge)으로 이루어진 자료구조의 일종을 말하며,그래프를 탐색한다는 것은 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하
velog.io
'Algorithm' 카테고리의 다른 글
| [python][백준] 1647번 도시분할계획 (0) | 2022.08.29 |
|---|---|
| [Algorithm] 유니온 파인드(Union-Find)란?? python에서 구현하기 (3) | 2022.08.26 |
| [python][프로그래머스] 체육복 (2) | 2022.07.29 |
| [python][프로그래머스] 크레인 인형뽑기 게임 (0) | 2022.07.27 |
| [python][프로그래머스] 큰수만들기 (0) | 2022.07.11 |
- Total
- Today
- Yesterday
- db
- PostgreSQL
- static files
- Linux
- lv1
- Master & Slave
- data formatting
- ORM
- react
- django
- list
- Algorithm
- lv2
- JavaScript
- uSWGI
- Default export
- docker
- union-find
- JS
- MVT
- 탐욕법
- container
- programmers
- Named export
- Greedy Algorithm
- Python
- generator expression
- This
- SQL
- django ORM
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
